Введение
Присмотритесь-ка к квадрату:
Он здоровый, тороватый,
Он надежнее как друг,
Чем уж слишком круглый круг.
В нем четыре стороны
И все стороны равны.
Честен каждою чертой,
Каждый угол в нем прямой.
Тем еще квадрат отличен,
Что вполне он симметричен,
Треугольников всех рать
Вам того не может дать.
Е. Паин
Правильные многоугольники с глубокой древности считались символом красоты и совершенства. Из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все углы. Одним из таких многоугольников является квадрат или другими словами, квадрат- это правильный четырехугольник.
Дать определение квадрату можно несколькими способами: квадрат – это прямоугольник, у которого все стороны равны и квадрат – это ромб, у которого все углы прямые.
Из школьного курса геометрии известно:
1 у квадрата все стороны равны,
2 все углы прямые,
3 диагонали равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
4 Квадрат обладает симметрией, которая придает ему простоту и известное совершенство формы: квадрат служит эталоном при измерении площадей всех фигур.
Это малая часть того, что можно раскрыть в этом вопросе, потому что современной математике известно достаточно много интересных и полезных свойств квадрата. Поэтому целью данного реферата является:
1 подробнее исследовать свойства квадрата,
2 рассмотреть геометрические способы раскроя квадрата,
3 обосновать возможности превращений фигур при помощи разрезания квадрата,
4 найти различные варианты построений, которые можно воспроизвести при помощи перегибания квадратного листа бумаги, и выявить преимущества в таком виде построений.
При изучении данной темы использовались статьи из книг и журналов, посвященных отдельным вопросам метематики.
В. Ф. Каган «О преобразовании многогранников». В этой книге приводится доказательство теоремы Ф. Больаи на примере квадрата.
В книге «Удивительный квадрат» Б.А. Кордемского и Н.В. Русалева подробно изложены доказательства некоторых свойств квадрата, приведены пример «совершенного квадрата» и решение одной задачи на разрезание квадрата арабским математиком Х века Абулом Вефой.
В книге И. Лемана «Увлекательная математика» собрано несколько десятков задач, среди которых есть и такие, возраст которых исчисляется тысячелетиями. Из этой книги в реферате были использованы задачи на разрезания квадрата.
Книги Я.И. Перельмана принадлежат к числу наиболее доступных из книг, посвященных занимательной математике. В книге «Занимательная геометрия» популярно изложен вопрос о фигурах с наибольшей площадью при данном периметре или с наименьшим периметром при данной площади.
Для полного представления о построении при помощи перегибания квадратного квадрата листа бумаги была использована книга И.Н. Сергеева «Примени математику».
ГЛАВА Ι. 1.1 ЗАМЕЧАТЕЛЬНЫЕ СВОЙСТВА КВАДРАТА
У квадрата есть два практичных свойства:
Периметр квадрата меньше периметра любого равновеликого ему прямоугольника,
Площадь квадрата больше площади любого прямоугольника с тем же периметром.
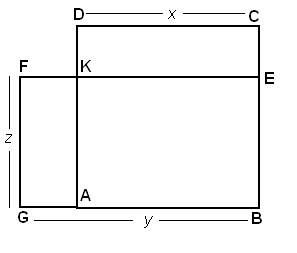
Рис.1
В своей книге «Удивительный квадрат» Б.А. Кордемский и Н.В. Русалев подробно описывают доказательства этих свойств.
Для доказательства первого свойства был сравнен периметр квадрата АВСD, со стороной x, данной площади (рис.1) с каким-либо прямоугольником ВЕFG,с большей стороной y, той же площади. Очевидно, что y больше x, ; тогда другая сторона z непременно меньше x. По чертежу видно, что АВЕК- общая часть и для квадрата и для прямоугольника; остаются два равновеликих прямоугольника АКFG и КЕСD, т.е. АG•FG = DС•КD. Но так как FG<DC, то AG>KD или y–x > x–z. Отсюда y+z>2x и 2y+2z>4x, то есть периметр любого прямоугольника, равновеликого квадрату, больше периметра квадрата. Значит, среди всех равновеликих прямоугольников квадрат обладает наименьшим периметром.
Для доказательства второго свойства авторы книги использовали метод, когда доказывают обратные теоремы – от противного.
Дан квадрат, периметр которого равен p, а площадь равна q.Пусть существует прямоугольник, периметр которого тоже равен p, а площадь Q>q. Затем авторы построили новый квадрат, равновеликий этому прямоугольнику, то есть с площадью, тоже равной Q, и, следовательно, большей, чем площадь данного квадрата. Но по предыдущей теореме периметр нового квадрата p <p.Значит, площадь нового квадрата больше площади данного, а периметр меньше. Это невозможно. Следовательно, не существует прямоугольника с периметром таким же, как у квадрата и площадью большей, чем площадь квадрата. Не существует также и прямоугольника, имеющего площадь, равную площади данного квадрата, так как в этом случае периметр квадрата меньше периметра прямоугольника, что противоречит условию.
Эти свойства можно считать практичными, потому что их можно использовать в жизненных ситуациях. Например, если нужно огородить изгородью, забором или решёткой участок земли определённой площади так, чтобы длина ограды была насколько возможно малой, причём огороженный участок должен быть прямоугольной формы, но с любым соотношением сторон. В переводе на точный, математический язык это значит: какой из прямоугольников данной площади имеет наименьший периметр?
В книге «Занимательная геометрия» Я.И. Перельмана приведены примеры и популярно изложены вопросы о фигурах с наибольшей площадью при данном периметре или с наименьшим периметре при данной площади
1.2 КВАДРАТ В КВАДРАТЕ
У квадрата, вписанного в квадрат, есть некоторые особенности.
а) б) б)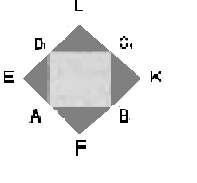 в) в)
Рис. 2.
Если соединить последовательно середины сторон квадрата АВСD (рис.2,а) отрезками, то получится новый квадрат ЕFКL, площадь которого составляет половину площади данного квадрата АВСD.
Если отрезать четыре прямоугольных треугольника, расположенных по углам квадрата АВСD. Сумма их площадей также составляет половину площади квадрата АВСD. Если принять площадь квадрата АВСD за единицу, то сумма площадей отрезанных треугольников равна Ѕ.
Если в оставшийся квадрат ЕРКL таким же образом вписать квадрат A B C D (рис. 2, б) и опять отрезать четыре треугольных уголка. Сумма площадей отрезанных треугольников составит Ѕ площади квадрата
ЕFKL и, значит, ј площади квадрата АВСD. Повторяя этот приём (рис.2,в), получается еще четвёрка треугольников, сумма площадей которых составит ⅛ площади квадрата АВСD.
Применяя этот приём любое число раз, будет получаться всё новые четвёрки прямоугольных треугольников, которыми снова можно выложить первоначальный квадрат. Суммы площадей четвёрок треугольников представляют бесконечный ряд чисел
Ѕ, ј ,⅛…
1.3 СОВЕРШЕННОЕ КВАДРИРОВАНИЕ
Эта любопытная задача долгое время не была решена, и многие думали, что её решить невозможно.
По содержанию это задача о составлении квадрата из нескольких квадратов, но на этот раз без разрезания их на части и усложнённая ещё требованием, чтобы стороны квадратов выражались неповторяющимися целыми числами. Число данных квадратов безразлично.
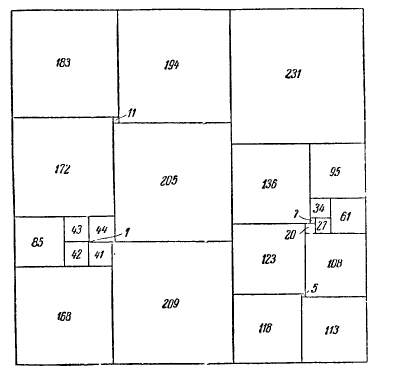
Рис.3
Деление квадрата на конечное число не налагающихся друг на друга квадратов, никакие два из которых не равны, называется совершенное квадрирование квадрата, а квадрат, составленный из неповторяющихся квадратов, - совершенным квадратом
Некоторые математики высказывали предположение, что совершенное квадрирование квадрата невозможно. Одним из таких математиков был Г. Штейнгауз, который утверждал в своей книге «Математический калейдоскоп», что «неизвестно, можно ли разбить квадрат на неповторяющиеся квадраты».
Так как это только допускалось математиками, но не было доказано, то поиски решения продолжались, и немногим более десяти лет тому назад в зарубежных математических журналах появились, наконец, квадраты, составленные из неповторяющихся квадратов. В своей книге «Удивительный квадрат» Кордемский Б.А. и Русалев Н.В. представили квадрат, состоящий из 26 неодинаковых квадратов(Рис.3). (Цифры, проставленные на рисунке, означают длины сторон соответствующих квадратов). Кордемский и Русалев пишут, что можно составить квадрат также и из 28 неповторяющихся квадратов и т. д.
Не вполне выясненным остаётся пока ещё вопрос о том, является ли 26 - наименьшим возможным числом квадратов для составления совершенного квадрата.
ГЛАВА ΙΙ. 2.1 ЗАДАЧА РАЗРЕЗЫВАНИЯ КВАДРАТА
Квадрат очень похож на механизм с хорошо прилаженными частями, который можно разобрать и из тех же частей собрать новый механизм.
Для того чтобы из готовых частей квадрата составить его снова или составить несколько иных, заранее указанных фигур, не нужны какие-либо расчёты и построения.
Из готовых частей квадрата можно сложить не только многоугольники, но и составить прямоугольный или равносторонний треугольник, правильный пятиугольник или шестиугольник, три или пять квадратов и т. д.
На языке геометрии это значит: найти те геометрические построения, при помощи которых разрезается квадрат, и доказать, что из полученных частей может быть составлена требуемая фигура.
Такая постановка вопроса сразу превращает каждую головоломку в более интересную, но и более трудную геометрическую задачу на «разрезывание» фигур. Своеобразие подобного рода задач в их некоторой неопределённости. Для примера, сформулируем головоломку из книги «Увлекательная математика» И.Лемана как следующую геометрическую задачу: показать, каким образом нужно разделить данный квадрат прямолинейными разрезами, чтобы переложением полученных частей можно было составить три сплошных квадрата, равных между собой.
В этой задаче ничего не сказано о том, как разрезать данный квадрат и на сколько частей,— отсюда и неопределённость.
Желательно, чтобы число разрезов было возможно меньшим, хотя заранее это число неизвестно, и неизвестно также, может ли оно быть установлено какими-либо предварительными расчётами. Обычно число делений зависит от способа разрезывания, то есть от тех геометрических построений, которые были применены при решении задачи.
В поисках наименьшего числа делений можно применять разнообразные приёмы построений и получать тем самым различные решения одной и той же задачи на разрезывание данной фигуры. Таким образом, при решении подобного рода задач открывается широкая возможность проявления находчивости и инициативы, развития геометрической интуиции.
2.2 КАК АБУЛ ВЕФА СОСТАВИЛ КВАДРАТ ИЗ ТРЁХ РАВНЫХ КВАДРАТОВ
Задачами превращения одной фигуры в другую путём переложения разрезанных частей занимались ещё в древние времена. Возникли они из потребностей практиков-землемеров и строителей архитектурных сооружений древнего мира. Появились практические приёмы и правила, не обоснованные доказательствами, и естественно, что многие из них были неверны, ошибочны.
Один из самых замечательных арабских математиков Абул Вефа, живший в X веке, решил целый ряд вопросов, относящихся к геометрическому превращению фигур. В сочинении «Книга о геометрических построениях», дошедшем до нас не полностью, в списках его учеников, Абул Вефа пишет:
«В настоящей книге мы займёмся разложением фигур; вопрос этот необходим многим практикам и составляет предмет особенных их разысканий. К таким вопросам мы приходим, когда требуется разложить квадраты так, чтобы получились меньшие квадраты, или когда из нескольких квадратов требуется составить большой квадрат. Ввиду этого мы дадим основные начала, которые относятся к данным вопросам, так как все методы, применяемые рабочими, не основанные на каких-либо началах, не заслуживают доверия и весьма ошибочны; между тем на основании таких методов они производят различные действия».
На одном из собраний геометров и практиков Абул Вефе была предложена задача:
Составить квадрат из трёх равных квадратов.
Абул Вефа разрезал квадраты I и II по диагоналям и каждую из половинок приложил к квадрату III, как показано на рис. 4.
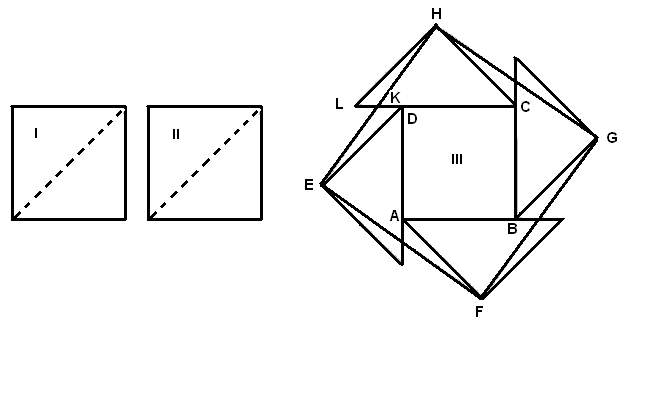
Рис.4
Затем он соединил отрезками прямых вершины Е, F, G и Н. Полученный четырёхугольник ЕFGН оказался искомым квадратом.
Доказательство сразу следует из равенства образовавшихся маленьких треугольников HLK, ЕКD и остальных таких же (НL=ED;углы HLK и EDK- по 45є и углы HKL и EKD равные).
Приведённое решение, по словам Абул Вефы, «точно и вместе с тем удовлетворяет практиков».
2.3 ВОЗМОЖНОСТЬ ПРЕВРАЩЕНИЙ КВАДРАТА
Решая головоломки и задачи на превращение квадрата в другую равновеликую ему фигуру путем разрезания или, наоборот, какого-либо многоугольника в квадрат, тем самым устанавливается возможность такого превращения.
Возникают вопросы, как далеко распространяется эта способность квадрата перекраиваться в другую фигуру без всякой потери площади.
Можно ли перекроить квадрат в любой желаемый многоугольник той же площади или, что то же самое,— можно ли любой многоугольник перекроить в равновеликий ему квадрат?
Ответ на эти вопросы даёт следующая теорема:
Всякий многоугольник можно превратить в равновеликий ему квадрат. Эта теорема рассматривается только для простых многоугольников.
В книге В.Ф. Каган «О Преобразовании многогранников» подробно описано доказательство теоремы Ф. Больан.
Основные ступени доказательства теоремы о возможности преобразования многоугольника в квадрат сформулировать в виде нескольких лемм:
1. Всякий многоугольник можно разрезать на некоторое определённое число треугольников.
2. Всякий треугольник равносоставлен с некоторым параллелограммом(два многоугольника называются равносоставленными, если один из них можно разрезать на такие части, которые, будучи сложены иначе, дают второй многоугольник.
Таким образом, каждый из треугольников, на которые рассекается многоугольник, можно превратить в параллелограмм.
Далее:
3. Всякий параллелограмм можно превратить в квадрат.
4. Если два многоугольника порознь могут быть превращены в третий, то первый может быть превращён во второй («свойство транзитивности»).
Из лемм 2, 3 и 4 следует пятая:
5. Всякий треугольник можно превратить в равновеликий ему квадрат.
6. Каждые два квадрата можно превратить в один.
Превращая каждые два квадрата в один, получается в конце концов один квадрат, который и будет равносоставлен с данным многоугольником.
В этом заключается доказательство возможности превращения многоугольника в квадрат, которая описывается в книге В.Ф. Кагана.
ГЛАВА ΙΙΙ. 3.1 ПОСТРОЕНИЯ ПРИ ПОМОЩИ ПЕРЕГИБАНИЯ КВАДРАТНОГО ЛИСТА БУМАГИ
Среди множества возможных действий с бумагой особое место занимает операция ее перегибания. Одним из достоинств этой операции является то, что ее можно производить, не имея под рукой никаких дополнительных инструментов - ни линейки, ни циркуля, ни даже карандаша. С помощью перегибания бумаги можно не только делать забавные или интересные игрушки, но и получать наглядное представление о многих фигурах на плоскости, а также об их свойствах
Практические свойства бумаги порождают своеобразную геометрию. Роль линий в этой геометрии будут играть края листа и складки, образующиеся при его перегибах, а роль точек - вершины углов листа и точки пересечения складок друг с другом или с краями листа. Оказывается, возможности операции перегибания листа очень велики. То, что они включают в себя всю геометрию одной линейки, не вызывает сомнения, Но они в определенной степени таят в себе также и возможности циркуля, хотя и не позволяют проводить непосредственно дуги окружности.
а) б)
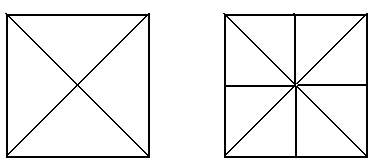
Рис. 5.
Исследуем некоторые свойства квадрата. Линия сгиба, проходящая через два противоположных угла квадрата, есть диагональ этого квадрата. Другая диагональ получается перегибом квадрата через другую пару противоположных углов, как это показано на рис 5а (линии внутри квадрата являются линиями сгиба). Каждая диагональ делит квадрат на два совпадающих при наложении треугольника, вершина которых находятся в противоположных углах квадрата. Эти треугольники равнобедренные и прямоугольные, так как каждый из них имеет по прямому углу.
Если перегнуть бумажный квадрат пополам, чтобы одна сторона совпадала с противоположною ей. Получится сгиб, проходящий через центр квадрата (рис.5б). Линия этого сгиба обладает следующими свойствами:
1) она перпендикулярна двум другим сторонам квадрата,
2) делит эти стороны пополам,
3) параллельно двум первым сторонам квадрата,
4) сама делится в центре квадрата пополам,
5) делит квадрат на два совпадающих при наложении прямоугольника, 6) каждый из этих прямоугольников равновелик (т. е. равен по площади) одному из треугольников, на которые квадрат делиться диагональю.
Если перегнуть квадрат еще раз так, чтобы совпадали две другие стороны, то полученный сгиб и сделанный раньше разделят квадрат на 4 совпадающих при наложении квадрата.
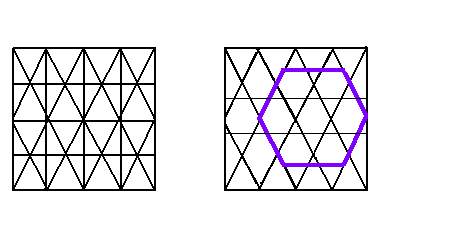
Пользуясь этими свойствами можно выполнять различные построения и превращения. Например, получить правильный шестиугольник. На рис.6а представлен образец орнамента из равносторонних треугольников и шестиугольников, полученных перегибанием квадратного листа бумаги. Эти многие другие построения подробно описываются и в книге «Примени математику» И.Н. Сергеева.
а) б)
Рис.6.
Можно разделить шестиугольник на равные правильные шестиугольники и равносторонние треугольники, делая перегибы через точки, делящие его стороны на три равные части. Получается красивый симметричный орнамент. Также при помощи перегибания квадратного листа бумаги можно построить биссектрису угла.
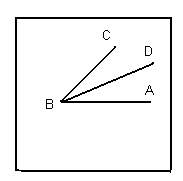
Рис.7
Следует отогнуть бумагу по прямым ВС и АВ (не на лицевую сторону), а затем перегибанием совместить отогнутый край ВС с отогнутым краем АВ. Получившийся сгиб ВD и будет биссектрисой угла АВС.(Рис.7)
При помощи перегибания квадратного листка бумаги можно произвести и довольно сложные построения. Например, произвести «золотое сечение» стороны данного квадратного куска бумаги при помощи только перегибаний.
Кстати, на основе перегибания квадратного листка бумаги возникло искусство оригами - складывание фигурок из бумаги (рис.8). Древнее искусство пришло из Китая, откуда Япония черпала духовные богатства. Квадрат выступает как оригинальный конструктор; его трансформируют бесконечно.



Рис 8.
ГЛАВА ΙV. 4.1 ТАНГРАМ И ДРУГИЕ ГОЛОВОЛОМКИ,
СВЯЗАННЫЕ С КВАДРАТОМ.
История головоломки "Танграм":

Головоломка "Танграм" - квадрат, разрезанный на 7 частей из которых составляют различные силуэты. Он появился в Китае в конце восемнадцатого века (рисунок). Первое ее изображение (1780 г.) обнаружено на ксилографии японского художника Утамаро, где две девушки складывают фигурки "чи чао ту" - так называется ташрам на его родине (в переводе - умственная головоломка из семи частей"). Название танграм возникло в Европе вероятнее всего от слова "тань" (на кантонском диалекте - китаец) и часто встречающегося греческого корня "грамма" (буква). Впрочем, авторы многих книг по занимательной математике приписывают изобретение танграма якобы жившему 4 тысячи лет назад в Китае ученому Тангу. Эта тщательно разработанная легенда от начала до конца выдумана изобретательным автором головоломок Сэмом Лойдом.
Вероятно, эти части квадрата первоначально служили для демонстрации фигур, потому что можно легко составить из частей квадрата прямоугольник, параллелограмм, трапецию и т. д. С течением времени было замечено, что из этих частей можно составить множество фигур-силуэтов (рис.9) самой причудливой формы, употребляя для составления каждой фигуры все семь частей квадрата. Изображение схематично, но образ легко угадывается по основным характерным признакам предмета, его строению, пропорциональному соотношению частей и форме. Составлять силуэты достаточно сложно. Сначала нужно найти сходство элементов с предметами, буквами и т.п. Затем можно составить силуэты игрушек, мебели, транспорта, животных.
Так создалась увлекательная игра-головоломка «танграм», получившая широкое распространение, в особенности на своей родине - в Китае. Там эта игра известно так же широко, как, например, у нас шахматы. Устраиваются даже специальные состязания на составление с наименьшей затратой времени.
Рисунки, составленные из частей танграма:
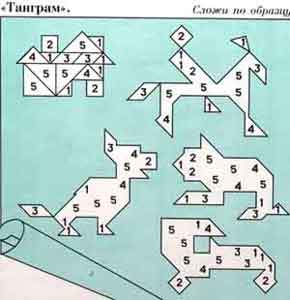 
Рис.9
Пентамино Эта игра была придумана в 50-х годах ХХ в. американским математиком С. Голомбом. Она заключается в складывании различных фигур из заданного набора пентамино. Набор содержит 12 фигурок, каждая из которых составлена из 5 одинаковых квадратов.
ЗАКЛЮЧЕНИЕ
Квадрат - это неисчерпаемая фигура, применяемая во многих сферах и имеющая свойства, интересные для каждого, кто стремится расширить рамки своих геометрических представлений.
В результате проделанной работы можно сформулировать несколько выводов:
1) периметр квадрата меньше периметра любого равновеликого ему прямоугольника;
2) площадь квадрата больше площади любого прямоугольника с тем же периметром;
3) при помощи разрезаний можно произвести превращения различных многоугольников в квадрат. Было установлено, что упражнения в разрезании квадрата и конструировании фигур из полученных частей являются не только полезной геометрической забавой, но имеют и практический смысл: они могут помочь будущим и настоящим новаторам производства, в рациональном раскрое материалов, в использовании обрезков кожи, ткани, дерева и т. п., для превращения их в полезные вещи;
4) при помощи перегибания квадратного листа бумаги можно выполнять различные построения, не имея под рукой никаких инструментов – ни линейки, ни циркуля, ни даже карандаша;
5) существуют занимательные игры, в которых используется квадрат.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1) Б.А. Кордемский, Н.В. Русалев «Удивительный квадрат». Москва-Ленинград, 1952 г.
2) В.Ф. Каган «О преобразовании многогранников». Гостехиздат, 1933 г.
3) Г. Штейнгауз «Математический калейдоскоп». Гостехиздат, 1949 г.
4) Е.И. Игнатьев « В царстве смекалки». Москва «Наука», 1981 г.
5) З.А. Михайлова «Игровые занимательные задачи для дошкольников». Москва «Просвещение», 1990 г.
6) И. Леман «Увлекательная математика». Москва «Наука» 1978 г.
7) И.Н. Сергеев «Примени математику». Москва «Наука», 1989 г.
8) «Квант» 1989. №5 – С. 40.
9) Р. Хонсбергер «Математические изюминки». Москва «Наука», 1992 г.
10) Я.И. Перельман «Живая математика». Москва «Наука», 1977 г.
11) Я.И Перельман «Занимательная геометрия». Москва «АСТ», 2003 г.
|